How to teach radicals in simplest form to your Geometry students (or any high school math student)…
In a high school geometry class, the need to simplify radicals (specifically square roots radicals) pops up from time to time. You’ll often encounter radicals when you teach the Geometric Mean Altitude Theorem and the Geometric Mean Leg Theorem (and among other topics, as well). When writing radicals in simplest form, you often end up with expressions like the square root of 48, for example, and because all math teachers feel compelled to simplify answers (it’s like an itch that has to be scratched), you encourage your students to write their final answers in simplified radical form.
You quickly realize that the words “simplified radical form” sound like Charlie Brown’s teacher to them. (“Wah, wah, wah, wah, wah, wah wah.”) So, always hopeful, you say, “You remember learning about simplified radical form in Algebra 1, right?” Crickets. Blank stares.
Time to pause and analyze the situation…
This is when you step out of your math teacher skin and step back into your kind, caring human skin. (Remember? That skin you put on in the morning, determined to be the empathetic teacher your students need. That “kindness skin” that has probably taken a few hits and is in tatters by this time of day.) You remember you are talking to teenagers. Of course they don’t remember simplifying radicals in Algebra 1. They barely remember what they had for breakfast! I feel you! It is tempting to roll your eyes and mumble to yourself, “Didn’t these kids learn anything last year?”, or, even worse, “They must have had a terrible teacher last year!” Instead, take a breath, and be kind! (And remember that they probably won’t remember what YOU are teaching them TODAY by this time next year! You aren’t a terrible teacher, are you?).
You might rather want to say something like, “If any of you remember how to simplify a square roots radical, that is really great! But for those of you who may have forgotten, let me remind you!” Put yourself in their shoes. (You were determined to be empathetic today, remember?). If you were a teenager, wouldn’t you feel better about yourself (and your teacher), if your teacher understands that you may not be able to recall one topic you learned on one day a year ago (in one of your seven classes). Wouldn’t you rather have a teacher who makes you feel safe from embarrassment because you know he or she will reteach the topic? So, just pause (don’t worry, you will still be able to finish today’s lesson) and take a few minutes to kindly answer the question, “How do I simplify radicals?” for your students before they ever ask!
So, let’s look at a couple of ways to remind your students how to write radicals in simplest form.
Simplifying radicals using the product of prime factors – good for younger grades
Teachers of younger students often teach simplifying square roots radicals using prime factors. It works great and is especially effective for lower grades. However, for high school students, I prefer a much quicker method, which I’ll explain later. First, let’s look at an example of simplifying a square root radical using prime factorization:
Example: To simplify the square root of 720 using prime factors, follow these steps:
1.) Start by dividing out the prime factors of 720, as many times as they occur, starting with 2 and working your way up:
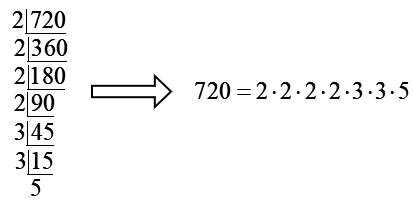
2.) Now, look for any pairs of prime factors and circle each pair.
![]()
3.) To find the square root of 720, bring one prime factor from each pair out from under the radical and leave any single prime factor(s) under the radical. Then simplify, if necessary
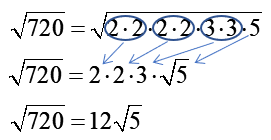
Here’s how students should check to see if they have written their radicals in simplest form. Teach them to look at the radicand (the number that remains under the radical symbol) and check to see if it has any factor (other than 1) that is a perfect square. In this example, the only factors of 5 are 5 and 1, so this radical is completely simplified. (Note: the radicand may or may not be a prime number.)
Students can be very successful simplifying radicals using the product of prime factors, but it does take a little time. As students get older and need to simplify square roots radicals in upper level math, a quicker method for writing radicals in simplest form might be preferred. So, let’s look at a quicker way.
Simplifying radicals finding hidden perfect squares and taking their roots…
For high school students (whose number sense is hopefully pretty decent – more on that later), I much prefer a quicker method to simplify radicals. It involves finding the largest perfect square factor of the radicand. If students can do that, then they can simplify a radical in a couple of quick steps.
Let’s look at the previous example and simplify it by finding the largest perfect square factor.
Example: To simplify the square root of 720 by finding the largest perfect square factor, follow these steps:
1.) Find the largest perfect square factor of 720. Be careful! There are more than one perfect square factors. You want the biggest one! (Have your students write out a list or table of perfect squares for reference. ) It might take a little trial and error, but they will quickly find that 144 is the largest factor of 720 that is a perfect square.
![]()
2.) Use this property of radicals:
![]()
and rewrite the square root of 720 as the product of the square roots of two factors, the first one being its largest perfect square factor.
![]()
3.) Simplify by taking the square root of the perfect square factor:
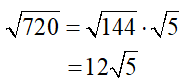
And just like that you are done! Quick and relatively easy!
A Superhero and Sidekick to the rescue for radicals in simplest form…
I like to call the previously described method the “Superhero and Sidekick Method.” Let me explain.
Before teaching this method, I show the kids a clip from the movie “Sky High”, a movie about the children of superheroes who attend high school at a school that floats up in the sky (hence the name). In the movie, when the students enter Sky High as freshmen, they attend an orientation where they must demonstrate their superpowers and are assigned either a “Superhero” status, or the “Sidekick” role (affectionately named “Hero Support” in the movie). I love the whole movie, but alas, usually only have time to show this one scene (found at about the 17 or so minute mark in the movie). And then I start teaching:
Example: “Let’s simplify the square root of 108”
Identify the characters:
Superhero: The largest factor of 108 that is a perfect square (enter 36)!
Sidekick: The other factor that will remain under the radical symbol (enter 3)!
So, to simplify the square root of 108, enter the Superhero….

The Superhero is….36, the largest factor of 108 and that is a perfect square.
And, our Superhero needs a Sidekick…
The Sidekick is…3, (Remember 108 is the product of 36 and 3).
Now, here’s how we will simplify the square root of 108:
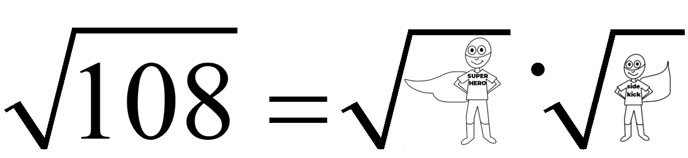
Actually, your students’ work should look like this:
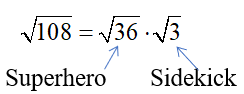
Note: be sure to always say “Let’s find the Superhero, which is the largest factor of the radicand that is a perfect square!” Don’t just say, “Let’s find the Superhero.” It’s always a good idea to use proper math vocabulary! You can say, “Superhero” as long as you also say, “the largest perfect square factor.”
So now, all that needs to be done is to simplify the square root of 36, which is a perfect square:
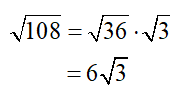
Voila! Done in two quick steps!
Let’s try another example.
Example: Let’s simplify the square root of 80 and write the answer in simplest radical form.
1.) Start by finding the “Superhero”, that is, the largest factor of 80 that is a perfect square. The largest perfect square factor of 80 is 16. (Remember, 16 is not the only perfect square factor, but it is the largest perfect square factor which is the one we want!)
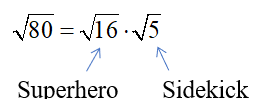
2.) Then, simplify the perfect square.
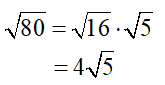
Quick and easy!
Show students the importance of finding the largest perfect square factor
Be sure to emphasize the need to find the largest perfect square factor, instead of just any perfect square factor. It’s good to demonstrate this for your students.
Let’s redo the last example (simplifying the square root of 80) and instead of identifying 16 (the “Superhero”), we instead choose 4, which is a perfect square factor of 80, but not the “Superhero”, (i.e. it’s not the largest perfect square factor of 80). (It’s not the “Sidekick”, either. Maybe it’s a “Superhero Wannabe”!)
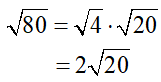
Check the radicand, 20. Because 20 has a factor that is a perfect square (4), this radical is not simplified and we need to keep going:
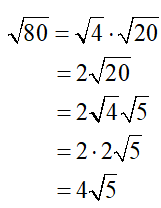
So, eventually, we got the most simplified answer, but it took several more steps because we did not identify the “Superhero”, the largest perfect square factor of 80, in the beginning! Just a reminder, encourage your students to check that their answers are simplified by always looking at the radicand (the number that remains under the radical), and making sure it has no factor (other than 1) that is a perfect square. The simplified radicand (i.e. the “Sidekick”) may or may not be a prime number.
Need a great resource for simplifying square roots radicals?
If you would like a lesson with guided notes and a practice worksheet to help your students master simplifying square roots radicals, I’ve got you covered! Check out this Guided Notes and Worksheet resource! Click here!

What about radicals other than square roots radicals?
Although I’ve demonstrated the “Superhero and Sidekick Method” of simplifying square roots radicals, this method could be used for all radicals. The only difference is in the definition of a “Superhero”. For example, if you are simplifying cube roots radicals, the “Superhero” would be the largest factor of the radicand that is a perfect cube!
Number sense: Students must first know square roots and perfect squares
A word about number sense. The “Superhero and Sidekick Method” for writing radicals in simplest form works best for students who are familiar with numbers that are perfect squares! I like my students to know perfect squares to at least 152.
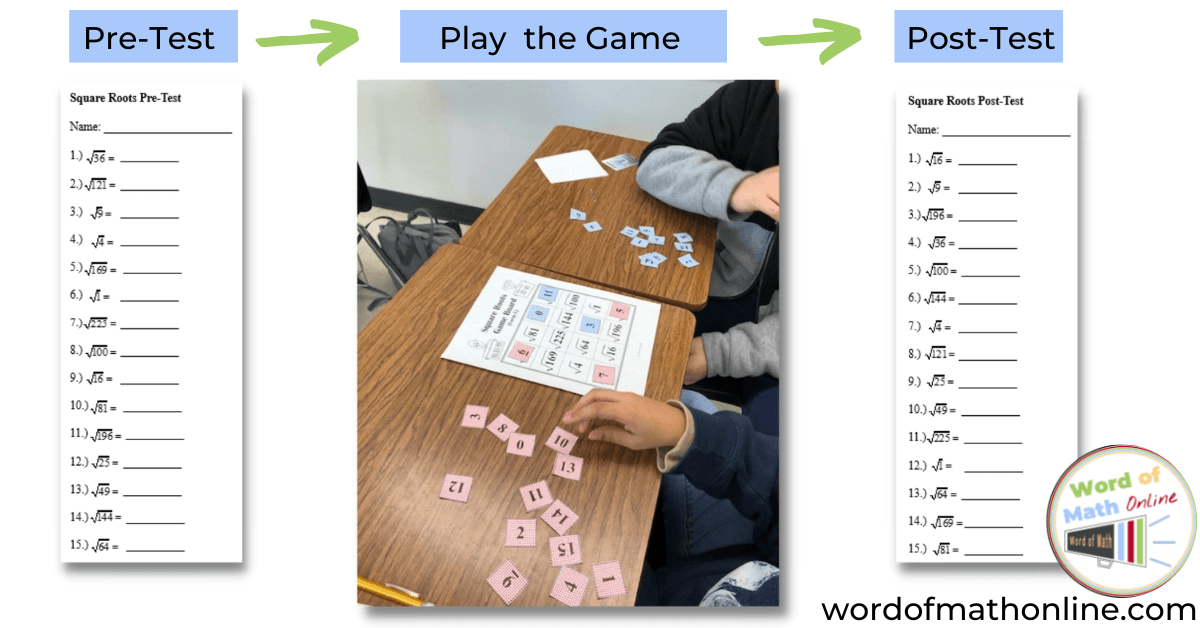
Before I teach a lesson on simplifying square roots, I leverage the power of games and competition to motivate students to become very familiar with numbers that are perfect squares, as well as their square roots.
I begin with a timed Pre-Test. Then, I have the students play a “4 in a Row” style game. To win the game, students are highly motivated to learn perfect squares and their square roots! The students play the game several times (keep switching out game boards). You might find that the students get a little creative and start making up new versions of the game. After several minutes of playing the game, I give the students a timed Post-Test. Almost all students make great improvement on the Post-Test!
This is a fun way to help students gain the number sense and confidence they need to be successful simplifying square roots radicals and writing radicals in simplest form! If you are interested in this resource (Pre-Test, Game (with instructions), Post-Test), click here to check it out! Your students will thank you!
Be your students’ Superhero…
Find a fun and engaging way to help your students know perfect squares and their square roots! Help them master simplifying square roots radicals! If you do, you will set them up to perform heroically when they encounter radicals in their upper level math classes! Good luck! I know you can do it!
P.S…
Could you use some great anytime, no prep Geometry freebies? Fill out the form below and I’ll send them to you right away!

P.S.S…
Are you looking for Geometry resources that will save you time and help you teach well? Then visit my Teachers Pay Teachers store. I am always adding new Geometry resources. You’ll find some Algebra 1 and Algebra 2 resources there, too!